HCL-Based Color Palettes • colorspace

Overview

As motivated in the previous article (Color Spaces: S4 Classes and Utilities), the HCL space is particularly useful for specifying individual colors and color palettes, as its three axes match those of the human visual system very well. Therefore, the colorspace package provides three types of palettes based on the HCL model:

Qualitative: Designed for coding categorical information, i.e., where no particular ordering of categories is available and every color should receive the same perceptual weight.
Sequential: Designed for coding ordered/numeric information, i.e., going from high to low (or vice versa).
Diverging: Designed for coding ordered/numeric information around a central neutral value, i.e., where colors diverge from neutral to two extremes.

The corresponding functions are qualitative_hcl(), sequential_hcl(), and diverging_hcl(). Their construction principles are exemplified in the following color swatches and explained in more detail below. The desaturated palettes bring out clearly that luminance differences (light-dark contrasts) are crucial for sequential and diverging palettes while qualitative palettes are balanced at the same luminance.

More details about the construction of such palettes is provided in the following while the article on Palette Visualization and Assessment introduces further tools to better understand the properties of color palettes.

To facilitate obtaining good sets of colors, HCL parameter combinations that yield useful palettes are accessible by name. These can be listed using the function hcl_palettes():

hcl_palettes()

## HCL palettes
## 
## Type:  Qualitative 
## Names: Pastel 1, Dark 2, Dark 3, Set 2, Set 3, Warm, Cold, Harmonic, Dynamic
## 
## Type:  Sequential (single-hue) 
## Names: Grays, Light Grays, Blues 2, Blues 3, Purples 2, Purples 3, Reds 2,
##        Reds 3, Greens 2, Greens 3, Oslo
## 
## Type:  Sequential (multi-hue) 
## Names: Purple-Blue, Red-Purple, Red-Blue, Purple-Orange, Purple-Yellow,
##        Blue-Yellow, Green-Yellow, Red-Yellow, Heat, Heat 2, Terrain,
##        Terrain 2, Viridis, Plasma, Inferno, Rocket, Mako, Dark Mint,
##        Mint, BluGrn, Teal, TealGrn, Emrld, BluYl, ag_GrnYl, Peach,
##        PinkYl, Burg, BurgYl, RedOr, OrYel, Purp, PurpOr, Sunset,
##        Magenta, SunsetDark, ag_Sunset, BrwnYl, YlOrRd, YlOrBr, OrRd,
##        Oranges, YlGn, YlGnBu, Reds, RdPu, PuRd, Purples, PuBuGn, PuBu,
##        Greens, BuGn, GnBu, BuPu, Blues, Lajolla, Turku, Hawaii, Batlow
## 
## Type:  Diverging 
## Names: Blue-Red, Blue-Red 2, Blue-Red 3, Red-Green, Purple-Green,
##        Purple-Brown, Green-Brown, Blue-Yellow 2, Blue-Yellow 3,
##        Green-Orange, Cyan-Magenta, Tropic, Broc, Cork, Vik, Berlin,
##        Lisbon, Tofino

To inspect the HCL parameter combinations for a specific palette simply include the palette name where upper- vs. lower-case, spaces, etc. are ignored for matching the label, e.g., "set2" matches "Set 2":

hcl_palettes(palette = "set2")

## HCL palette
## Name: Set 2
## Type: Qualitative
## Parameter ranges:
##  h1 h2 c1 c2 l1 l2 p1 p2 cmax fixup
##   0 NA 60 NA 70 NA NA NA   NA  TRUE

To compute the actual color hex codes (representing sRGB coordinates), the functions qualitative_hcl(), sequential_hcl(), and diverging_hcl(), respectively, can be used. Either all parameters can be specified “by hand” through the HCL parameters, an entire palette can be specified “by name”, or the name-based specification can be modified by a few HCL parameters. In case of the HCL parameters, either a vector-based specification such as h = c(0, 270) or individual parameters h1 = 0 and h2 = 270 can be used.

The first three of the following commands lead to equivalent output. The fourth command yields a modified set of colors (lighter due to a luminance of 80 instead of 70).

qualitative_hcl(4, h = c(0, 270), c = 60, l = 70)

## [1] "#ED90A4" "#ABB150" "#00C1B2" "#ACA2EC"

qualitative_hcl(4, h1 = 0, h2 = 270, c1 = 60, l1 = 70)

## [1] "#ED90A4" "#ABB150" "#00C1B2" "#ACA2EC"

qualitative_hcl(4, palette = "set2")

## [1] "#ED90A4" "#ABB150" "#00C1B2" "#ACA2EC"

qualitative_hcl(4, palette = "set2", l = 80)

## [1] "#FFACBF" "#C6CD70" "#32DDCD" "#C7BEFF"

Qualitative palettes

qualitative_hcl() distinguishes the underlying categories by a sequence of hues while keeping both chroma and luminance constant, to give each color in the resulting palette the same perceptual weight. Thus, h should be a pair of hues (or equivalently h1 and h2 can be used) with the starting and ending hue of the palette. Then, an equidistant sequence between these hues is employed, by default spanning the full color wheel (i.e., the full 360 degrees). Chroma c (or equivalently c1) and luminance l (or equivalently l1) are constants. Finally, fixup indicates whether colors with out-of-range coordinates should be corrected.

In the following graphic the available named palettes are shown. The first five palettes are close to the ColorBrewer.org palettes of the same name (Harrower and Brewer 2003). They employ different levels of chroma and luminance and, by default, span the full hue range. The remaining four palettes are taken from Ihaka (2003). They are based on the same chroma (50) and luminance (70) but the hue is restricted to different intervals.

hcl_palettes("qualitative", plot = TRUE)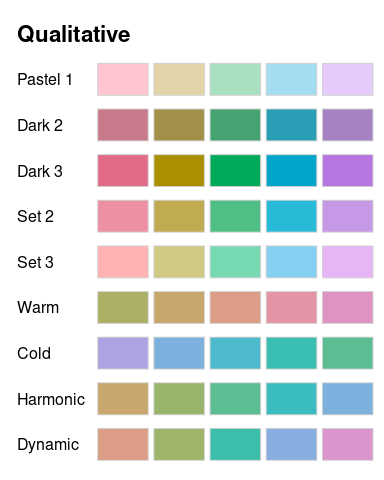

When palettes are employed for shading areas in statistical displays (e.g., in bar plots, pie charts, or regions in maps), lighter colors (with moderate chroma and high luminance) such as “Pastel 1” or “Set 3” are typically less distracting. By contrast, when coloring points or lines, more flashy colors (with high chroma) are often required: On a white background a moderate luminance as in “Dark 2” or “Dark 3” usually works better while on a black/dark background the luminance should be higher as in “Set 2” for example.

Sequential palettes (single-hue)

sequential_hcl() codes the underlying numeric values by a monotonic sequence of increasing (or decreasing) luminance. Thus, the function’s l argument should provide a vector of length 2 with starting and ending luminance (equivalently, l1 and l2 can be used). Without chroma (i.e., c = 0), this simply corresponds to a grayscale palette like gray.colors(), see “Grays” and “Light Grays” below.

For adding chroma, a simple strategy would be to pick a single hue (via h or h1) and then decrease chroma from some value (c or c1) to zero (i.e., gray) along with increasing luminance. This is already very effective for bringing out the extremes (a dark high-chroma color vs. a light gray), see "Blues 2", "Purples 2", "Reds 2", and "Greens 2".

For distinguishing colors in the middle, two strategies can be employed: (a) Hue can be varied as well by specifying an interval of hues in h (or beginning hue h1 and ending hue h2). More details are provided in the next section. (b) Instead of a decreasing chroma, a triangular chroma trajectory can be employed from c1 over cmax to c2 (equivalently specified as a vector c of length 3). This yields high-chroma colors in the middle of the palette that are more easily distinguished from the dark and light extremes. See “Blues 3”, “Purples 3”, “Reds 3”, and “Greens 3” below.

Instead of employing linear trajectories in the chroma or luminance coordinates, some palettes employ a power transformation of the chroma and/or luminance trajectory. Either a vector power of length 2 or separate p1 (for chroma) and p2 (for luminance) can be specified. If the latter is missing, it defaults to the former.

hcl_palettes("sequential (single-hue)", n = 7, plot = TRUE)

All except the last are inspired by the ColorBrewer.org palettes with the same base name (Harrower and Brewer 2003) but restricted to a single hue only. They are intended for a white/light background. The last palette (Oslo) is taken from the scientific color maps of Crameri (2018) and is intended for a black/dark background and hence the order is reversed starting from a light blue (not a light gray).

To distinguish many colors in a sequential palette it is important to have a strong contrast on the luminance axis, possibly enhanced by an accompanying pronounced variation in chroma. When only a few colors are needed (e.g., for coding an ordinal categorical variable with few levels) then a lower luminance contrast may suffice.

Sequential palettes (multi-hue)

To not only bring out extreme colors in a sequential palette but also better distinguish middle colors it is a common strategy to employ a sequence of hues. Thus, the basis of such a palette is still a monotonic luminance sequence as above (combined with a monotonic or triangular chroma sequence). But rather than using a single hue, an interval of hues in h (or beginning hue h1 and ending hue h2) can be specified.

sequential_hcl() allows combined variations in hue (h and h1/h2, respectively), chroma (c and c1/c2/cmax, respectively), luminance (l and l1/l2, respectively), and power transformations for the chroma and luminance trajectories (power and p1/p2, respectively). This yields a broad variety of sequential palettes, including many that closely match other well-known color palettes. The plot below shows all the named multi-hue sequential palettes in colorspace:

“Purple-Blue” to “Terrain 2” are various palettes created during the development of colorspace, e.g., by Zeileis, Hornik, and Murrell (2009) or Stauffer et al. (2015) among others.
“Viridis” to “Inferno” closely match the palettes that Smith and Van der Walt (2015) developed for matplotlib and that gained popularity recently.
“Dark Mint” to “BrwnYl” closely match palettes provided in CARTO (CARTO 2019).
“YlOrRd” to “Blues” closely match ColorBrewer.org palettes (Harrower and Brewer 2003).
“Lajolla” to “Batlow” closely match the scientific color maps of the same name by Crameri (2018) and the first two of these are intended for a black/dark background.

hcl_palettes("sequential (multi-hue)", n = 7, plot = TRUE)

Note that the palettes differ substantially in the amount of chroma and luminance contrasts. For example, many palettes go from a dark high-chroma color to a neutral low-chroma color (e.g., “Reds”, “Purples”, “Greens”, “Blues”) or even light gray (e.g., “Purple-Blue”). But some palettes also employ relatively high chroma throughout the palette (e.g., the viridis and many CARTO palettes). To emphasize the extremes the former strategy is typically more suitable while the latter works better if all values along the sequence should receive some more perceptual weight.

Diverging palettes

diverging_hcl() codes the underlying numeric values by a triangular luminance sequence with different hues in the left and in the right “arms” of the palette. Thus, it can be seen as a combination of two sequential palettes with some restrictions: (a) a single hue is used for each arm of the palette, (b) chroma and luminance trajectory are balanced between the two arms, (c) the neutral central value has zero chroma. To specify such a palette a vector of two hues h (or equivalently h1 and h2), either a single chroma value c (or c1) or a vector of two chroma values c (or c1 and cmax), a vector of two luminances l (or l1 and l2), and power parameter(s) power (or p1 and p2) are used. For more flexible diverging palettes without the restrictions above (and consequently more parameters) see the divergingx_hcl() palettes introduced below.

The plot below shows all such diverging palettes that have been named in colorspace:

“Blue-Red” to “Cyan-Magenta” have been developed for colorspace starting from Zeileis, Hornik, and Murrell (2009), taking inspiration from various other palettes, including more balanced and simplified versions of several ColorBrewer.org palettes (Harrower and Brewer 2003).
“Tropic” closely matches the palette of the same name from CARTO (CARTO 2019).
“Broc” to “Vik” and “Berlin” to “Tofino” closely match the scientific color maps of the same name by Crameri (2018), where the first three are intended for a white/light background and the other three for a black/dark background.

hcl_palettes("diverging", n = 7, plot = TRUE)

When choosing a particular palette for a display similar considerations apply as for the sequential palettes. Thus, large luminance differences are important when many colors are used while smaller luminance contrasts may suffice for palettes with fewer colors etc.

Construction details

The three different types of palettes (qualitative, sequential, and diverging) are all constructed by combining three different types of trajectories (constant, linear, triangular) for the three different coordinates (hue H, chroma C, luminance L):

Type	H	C	L
Qualitative	Linear	Constant	Constant
Sequential	Constant (single-hue) or Linear (multi-hue)	Linear (+ power) or Triangular (+ power)	Linear (+ power)
Diverging	Constant (2x)	Linear (+ power) or Triangular (+ power)	Linear (+ power)

As pointed out initially in this article, luminance is probably the most important property for defining the type of palette. It is constant for qualitative palettes, monotonic for sequential palettes (linear or a power transformation), and uses two monotonic trajectories (linear or a power transformation) diverging from the same neutral value.

Hue trajectories are also rather intuitive and straightforward for the three different types of palettes. However, chroma trajectories are probably the most complicated and least obvious from the examples above. Hence, the exact mathematical equations underlying the chroma trajectories are given in the following (i.e., using the parameters c1, c2, cmax, and p1, respectively). Analogous equations apply for the other two coordinates.

The trajectories are functions of the intensity \(i \in [0, 1]\) where \(1\) corresponds to the full intensity:

\[ \begin{align*} \text{Constant: } & c_1 \\[0.2cm] \text{Linear: } & c_2 - (c_2 - c_1) \cdot i \\[0.2cm] \text{Triangular: } & \left\{ \begin{array}{lcl} c_2 - (c_2 - c_\max) \cdot \frac{i}{j} & \text{if } i & \le j \\ c_\max - (c_\max - c_1) \cdot \frac{i - j}{1 - j} & & > j \end{array} \right. \end{align*} \]

where \(j\) is the intensity at which \(c_\max\) is assumed. It is constructed such that the slope to the left is the negative of the slope to the right of \(j\):

\[ j = \left(1 + \frac{|c_\max - c_1|}{|c_\max - c_2|} \right)^{-1} \]

Instead of using a linear intensity \(i\) going from \(1\) to \(0\), one can replace \(i\) with \(i^{p_1}\) in the equations above. This then leads to power-transformed curves that add or remove chroma more slowly or more quickly depending on whether the power parameter \(p_1\) is \(< 1\) or \(> 1\).

The three types of trajectories are also depicted below. Note that full intensity \(i = 1\) is on the left and zero intensity \(i = 0\) is on the right of each panel.

The concrete parameters in the plot above are:

Constant: c1 = 80.
Linear: c1 = 80, c2 = 10, p1 = 1 (solid) vs. p1 = 1.6 (dashed).
Triangular: c1 = 60, cmax = 80, c2 = 10, p1 = 1 (solid) vs. p1 = 1.6 (dashed).

Further discussion of these trajectories and how they can be visualized and assessed for a given color palette is provided in the article: Palette Visualization and Assessment.

Registering your own palettes

The hcl_palettes() already come with a wide range of predefined palettes to which customizations can be easily added. However, it might also be convenient to register a custom palette so that it can subsequently be reused with a new dedicated name. This is supported by adding a register argument once to a call to qualitative_hcl(), sequential_hcl(), or diverging_hcl():

qualitative_hcl(3, palette = "set2", l = 80, register = "myset")

The new palette is then included in hcl_palettes():

hcl_palettes("Qualitative")

## HCL palettes
## 
## Type:  Qualitative 
## Names: Pastel 1, Dark 2, Dark 3, Set 2, Set 3, Warm, Cold, Harmonic, Dynamic,
##        myset

The palette can be used subsequently in qualitative_hcl() as well as the qualitative ggplot2 color scales, e.g.,

qualitative_hcl(4, palette = "myset")

## [1] "#FFACBF" "#C6CD70" "#32DDCD" "#C7BEFF"

Remarks:

The number of colors in the palette that was used during registration is not actually stored and can be modified subsequently. The same holds for arguments alpha and rev.
When registering a new palette with a previously-used name, the old palette gets overwritten. We recommend to not overwrite the palettes that are predefined in the package (albeit technically possible).
The registration of a palette is only stored for the current session. When R is restarted and/or the colorspace package reloaded, only the predefined palettes from the package are available. Thus, to make a palette permanently available a registration R code like colorspace::qualitative_hcl(3, palette = "set2", l = 80, register = "myset") can be placed in your .Rprofile or similar startup scripts.

Flexible diverging palettes

The divergingx_hcl() function provides more flexible diverging palettes by simply calling sequential_hcl() twice with prespecified sets of hue, chroma, and luminance parameters. Thus, it does not pose any restrictions that the two “arms” of the palette need to be balanced and also may go through a non-gray neutral color (typically light yellow). Consequently, the chroma/luminance paths can be rather unbalanced.

The plot below shows all such flexible diverging palettes that have been named in colorspace:

“ArmyRose” to “Tropic” closely match the palettes of the same name from CARTO (CARTO 2019).
“PuOr” to “Spectral” closely match the palettes of the same name from ColorBrewer.org (Harrower and Brewer 2003).
“Zissou 1” closely matches the palette of the same name from wesanderson (Ram and Wickham 2018).
“Cividis” closely matches the palette of the same name from the viridis family (Garnier 2018). Note that despite having two “arms” with blue vs. yellow colors and a low-chroma center color, this is probably better classified as a sequential palette due to the monotonic chroma going from dark to light. (See Approximating Palettes from Other Packages for more details.)
“Roma” closely matches the palette of the same name by Crameri (2018).

divergingx_palettes(n = 7, plot = TRUE)

Typically, the more restricted diverging_hcl() palettes should be preferred because they are more balanced. However, by being able to go through light yellow as the neutral color warmer diverging palettes are available.

HCL (and HSV) color palettes corresponding to base R palettes

To facilitate switching from base R palette functions to the HCL-based palettes above, colorspace provides a few convenience interfaces:

rainbow_hcl(): Convenience interface to qualitative_hcl() for a HCL-based “rainbow” palette to replace the (in)famous rainbow() palette.
heat_hcl(): Convenience interface to sequential_hcl() with default parameters chosen to generate more balanced heat colors than the basic heat.colors() function.
terrain_hcl(): Convenience interface to sequential_hcl() with default parameters chosen to generate more balanced terrain colors than the basic terrain.colors() function.
diverging_hsv(): Diverging palettes generated in HSV space rather than HCL space as in diverging_hcl(). This is provided for didactic purposes to contrast the more balanced HCL palettes with the more flashy and unbalanced HSV palettes.

Meanwhile, base R has also adopted the HCL-based palettes from colorspace into the function hcl.colors() in grDevices (Zeileis and Murrell 2019). This provides all the named palettes introduced in colorspace (with the same names) but without the flexibility to modify or adapt existing palettes.

Moreover, the grDevices package in base R gained a new function palette.colors() (Zeileis et al. 2019) that provides various well-established qualitative color palettes that can not be approximated well by qualitative_hcl() due to pronounced variations in luminance and chroma. While a qualitative palette with fixed luminance and chroma is more balanced, a certain amount of variations in these properties might be necessary to make more colors distinguishable, especially for viewers with color vision deficiencies.

References

CARTO. 2019. “CARTOColors – Data-Driven Color Schemes.” https://carto.com/carto-colors/.

Crameri, Fabio. 2018. “Geodynamic Diagnostics, Scientific Visualisation and StagLab 3.0.” Geoscientific Model Development 11 (6): 2541–62. https://doi.org/10.5194/gmd-11-2541-2018.

Garnier, Simon. 2018. Viridis: Default Color Maps from Matplotlib. https://CRAN.R-project.org/package=viridis.

Harrower, Mark A., and Cynthia A. Brewer. 2003. “ColorBrewer.org: An Online Tool for Selecting Color Schemes for Maps.” The Cartographic Journal 40 (1): 27–37. https://doi.org/10.1179/000870403235002042.

Ihaka, Ross. 2003. “Colour for Presentation Graphics.” In Proceedings of the 3rd International Workshop on Distributed Statistical Computing, Vienna, Austria, edited by Kurt Hornik, Friedrich Leisch, and Achim Zeileis. https://www.r-project.org/conferences/DSC-2003/Proceedings/Ihaka.pdf.

Ram, Karthik, and Hadley Wickham. 2018. Wesanderson: A Wes Anderson Palette Generator. https://CRAN.R-project.org/package=wesanderson.

Smith, Nathaniel, and Stéfan Van der Walt. 2015. “A Better Default Colormap for Matplotlib.” In SciPy 2015 – Scientific Computing with Python. Austin. https://www.youtube.com/watch?v=xAoljeRJ3lU.

Stauffer, Reto, Georg J. Mayr, Markus Dabernig, and Achim Zeileis. 2015. “Somewhere over the Rainbow: How to Make Effective Use of Colors in Meteorological Visualizations.” Bulletin of the American Meteorological Society 96 (2): 203–16. https://doi.org/10.1175/BAMS-D-13-00155.1.

Zeileis, Achim, Kurt Hornik, and Paul Murrell. 2009. “Escaping RGBland: Selecting Colors for Statistical Graphics.” Computational Statistics & Data Analysis 53: 3259–70. https://doi.org/10.1016/j.csda.2008.11.033.

Zeileis, Achim, and Paul Murrell. 2019. “HCL-Based Color Palettes in grDevices.” https://developer.R-project.org/Blog/public/2019/04/01/hcl-based-color-palettes-in-grdevices/.

Zeileis, Achim, Paul Murrell, Martin Maechler, and Deepayan Sarkar. 2019. “A New palette() for .” https://developer.R-project.org/Blog/public/2019/11/21/a-new-palette-for-r/.